First Steps with Choco

The problem consists in filling a NxN grid with the numbers 1, 2, . . . , N such that each row and column has the same sum.

Let's create a new class MagicSquare in a file MagicSquare.java:

import choco.integer.IntVar;
import choco.Problem;

public class MagicSquare {

  public static void main(String[] args) {
    int n = 4;
    System.out.println("Magic Square Problem with n = " + n);
  }
}

We will now complete this main method.

Create the problem

First a new problem must be created. Creation of variables and constraints are based on the Problem object. Therefore, it is a central element of your choco program.

    Problem myPb = new Problem(); 

Create variables

Variables have to be created for this problem. As we deal with discrete domains to fill the magic grid, EnumIntVar variables will be used. Bounds Variables called BoundIntVar exist and can be used for larger domains. A table of size NxN is created here and a variable is associated to each cell of the grid. The name of the variable, the lower and upper bounds of its enumerated domain are given in argument of the variable constructor. Notice that one more variable, sum, indicating the sum of lines and rows will be needed.

    IntVar[] vars = new IntVar[n * n];
    for (int i = 0; i < n; i++)
      for (int j = 0; j < n; j++) {
        vars[i * n + j] = myPb.makeEnumIntVar("C" + i + "_" + j, 1, n * n);
      }
    IntVar sum = myPb.makeEnumIntVar("S", 1, n * n * (n * n + 1) / 2);

Add constraints

Again, the Problem instance is responsible for creating and posting the constraints: Firstly, all the cells of the grid have to take different values. Our variables should therefore be pairwise distinct :

    for (int i = 0; i < n * n; i++)
      for (int j = 0; j < i; j++)
        myPb.post(myPb.neq(vars[i], vars[j]));

Secondly, the variable sum is linked to the variables of each lines and rows. A scalar product with coefficients equal to 1 is used to ensure that the sum of each line and row will be equal to the same value (notice that a sum constraint is available as a shorthand).

    int[] coeffs = new int[n];
    for (int i = 0; i < n; i++) {
      coeffs[i] = 1;
    }

    for (int i = 0; i < n; i++) {
      IntVar[] col = new IntVar[n];
      IntVar[] row = new IntVar[n];

      for (int j = 0; j < n; j++) {
        col[j] = vars[i * n + j];
        row[j] = vars[j * n + i];
      }

      myPb.post(myPb.eq(myPb.scalar(coeffs, row), sum));
      myPb.post(myPb.eq(myPb.scalar(coeffs, col), sum));
    }

Finally, the value of the sum can be specified and should be equal to N*(N*N + 1) / 2. This constraint is a redundant one that ensure a stronger propagation. It can be omitted.

    myPb.post(myPb.eq(sum, n * (n*n + 1) / 2));

We can now either search for one solution, or all solutions of the problem.

Searching one solution

The first solution can be obtained with a simple call to the solve() method. It will give the first solution found by the solver and stop the search.

    myPb.solve();

Searching all solutions

To search all solutions, the solveAll() method can be called:

    problem.solveAll();

We can now use the solver instance to know how many solutions were found. For instance, let's display the number of solutions:

    System.out.println("Solution number: " +
      problem.getSolver().getNbSolutions());

Let's see what our choco program looks like :

import choco.integer.IntVar;
import choco.Problem;

public class MagicSquare {

  public static void main(String[] args) {
    int n = 4;
    System.out.println("Magic Square Problem with n = " + n);

    Problem myPb = new Problem();

    IntVar[] vars = new IntVar[n * n];
    for (int i = 0; i < n; i++)
      for (int j = 0; j < n; j++) {
        vars[i * n + j] = myPb.makeEnumIntVar("C" + i + "_" + j, 1, n * n);
      }
    IntVar sum = myPb.makeEnumIntVar("S", 1, n * n * (n * n + 1) / 2);

    myPb.post(myPb.eq(sum, n * (n*n + 1) / 2));
    for (int i = 0; i < n * n; i++)
      for (int j = 0; j < i; j++)
        myPb.post(myPb.neq(vars[i], vars[j]));

    int[] coeffs = new int[n];
    for (int i = 0; i < n; i++) {
      coeffs[i] = 1;
    }

    for (int i = 0; i < n; i++) {
      IntVar[] col = new IntVar[n];
      IntVar[] row = new IntVar[n];

      for (int j = 0; j < n; j++) {
        col[j] = vars[i * n + j];
        row[j] = vars[j * n + i];
      }

      myPb.post(myPb.eq(myPb.scalar(coeffs, row), sum));
      myPb.post(myPb.eq(myPb.scalar(coeffs, col), sum));
    }
    myPb.solve();
  }

}

Like all Java programs, executing this code needs to compile and launch it. If your CLASSPATH variable points to the Choco jar file, the following command allows to compile this sample class: javac MagicSquare.java.

If your CLASSPATH does not contain the Choco package, please read the page about installation or use the -classpath option: javac -classpath $CLASSPATH;/path/to/jar/file MagicSquare.java (with semi-columns with Windows environment and columns for UNIX like environements).

Last, to launch the main method, you only need to call: java MagicSquare. Again, if your CLASSPATH is not set up, you can use the -cp option. Here is how the result should look like:

>java MagicSquare
Magic Square Problem with n = 4
Pb[17 vars, 129 cons]
C0_0{1}
C0_1{2}
C0_2{15}
C0_3{16}
C1_0{6}
C1_1{11}
C1_2{10}
C1_3{7}
C2_0{13}
C2_1{9}
C2_2{4}
C2_3{8}
C3_0{14}
C3_1{12}
C3_2{5}
C3_3{3}
S{34}

-- solve => 1 solutions
-- 172[+0] millis.
-- 9[+0] nodes

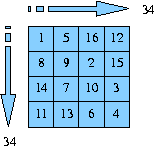
Each solution is displayed as soon as it is found. The solution found here corresponds to the square displayed in the previous figure. We could ask for all solutions and display the number of solutions. Last, the log information is displayed asynchronously; here the log indicates the solution number and the time and node number needed to find the first solution.

Choco contains an explanation based solver based on PaLM. Switchintg from choco to Palm only require to change the type of the problem object. Since the PaLM problem inherits from the Choco one, all problem modelling is similar. For instance, you can use mac-dbt algorithm by adding this import import choco.palm.*; and by modifying the line creating the problem instance: Problem myPb = new PalmProblem();. The rest of the code remains unchanged.

Of course using explanations is more usefull when you want to know why a value is removed from a variable's domain. For instance, if one want to know why var3 can not equal 1, the following lines can be added (see the complete code for the dependent imports):

    Explanation expl = ((PalmProblem)problem).makeExplanation();
    ((PalmIntVar)vars[3]).self_explain(PalmIntDomain.VAL, 1, expl);
    System.out.println("Why " + vars[3] + " != 1 : " + expl);

The first line creates an explanation instance which is an entity able to store information explaining an inference: a set of constraints. The second line update this explanation with the explanation of the missing value 1 in the variable domain of the cell 3. Last, this explanation is displayed.

The complet code is now:

import choco.Problem;
import choco.integer.IntVar;
import choco.palm.PalmProblem;
import choco.palm.integer.PalmIntVar;
import choco.palm.integer.PalmIntDomain;
import choco.palm.explain.Explanation;

public class MagicSquare {

  public static void main(String[] args) {
    int n = 4;
    System.out.println("Magic Square Problem with n = " + n);

    Problem myPb = new PalmProblem();

    IntVar[] vars = new IntVar[n * n];
    for (int i = 0; i < n; i++)
      for (int j = 0; j < n; j++) {
        vars[i * n + j] = myPb.makeEnumIntVar("C" + i + "_" + j, 1, n * n);
      }
    IntVar sum = myPb.makeEnumIntVar("S", 1, n * n * (n * n + 1) / 2);

    myPb.post(myPb.eq(sum, n * (n*n + 1) / 2));
    for (int i = 0; i < n * n; i++)
      for (int j = 0; j < i; j++)
        myPb.post(myPb.neq(vars[i], vars[j]));

    int[] coeffs = new int[n];
    for (int i = 0; i < n; i++) {
      coeffs[i] = 1;
    }

    for (int i = 0; i < n; i++) {
      IntVar[] col = new IntVar[n];
      IntVar[] row = new IntVar[n];

      for (int j = 0; j < n; j++) {
        col[j] = vars[i * n + j];
        row[j] = vars[j * n + i];
      }

      myPb.post(myPb.eq(myPb.scalar(coeffs, row), sum));
      myPb.post(myPb.eq(myPb.scalar(coeffs, col), sum));
    }

    myPb.solve();

    Explanation expl = ((PalmProblem)myPb).makeExplanation();
    ((PalmIntVar)vars[3]).self_explain(PalmIntDomain.VAL, 2, expl);
    System.out.println("Why " + vars[3] + " =! 2 : " + expl);

  }

The execution of this code should look like:

>java Sample
Magic Square Problem with n = 4
** JPaLM : Constraint Programming with Explanations
** JPaLM v0.1 (September, 2003), Copyright (c) 2000-2003 N. Jussien
Why C0_3 =! 1 : {C0_3 !== C0_0 + 0, C0_0 == 1}

This shows that var3 can not equal to 1 because of two constraints:

• C0_3 !== C0_1
• C0_0 == 1

Notice that the second constraint is a decision taken during search by the solver. Indeed since var0 is equal to 1 and var3 has to be distinct of var0, it can not be equal to 1.