Choco Performance Report
Benchmark Description
The benchmarck is done on a Pentium 4 3Gh, 512 Mo with the sun jdk1.4.2_03 in server mode (-server). The stack size used is the default jvm size (no -X options).
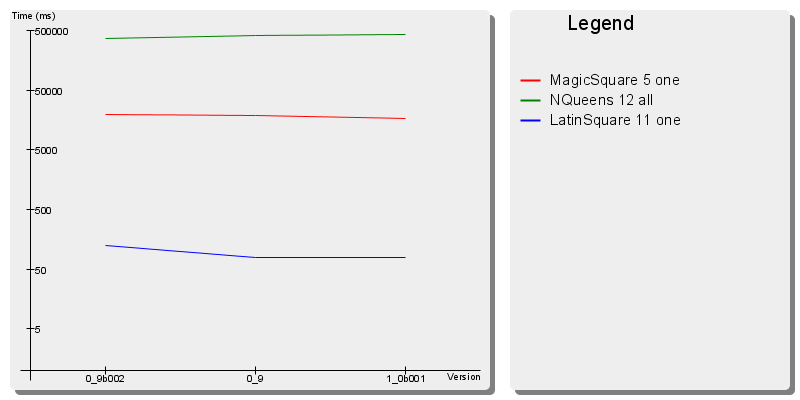
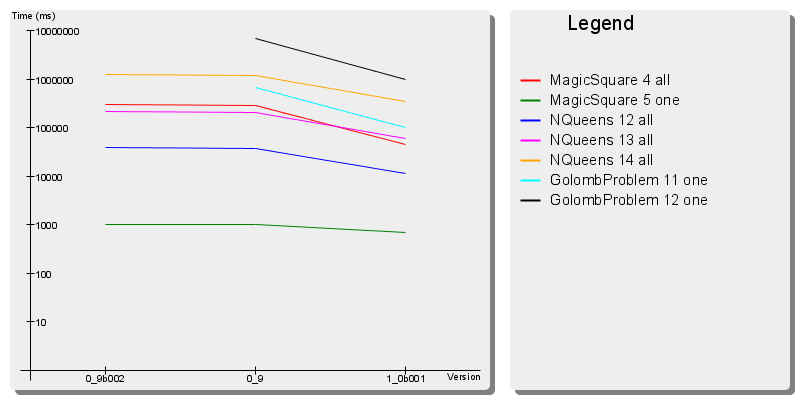
N Queens
The problem is modeled with N integer variables of domain 1 .. N corresponding to each line of the board, and only inequality constraints are used.
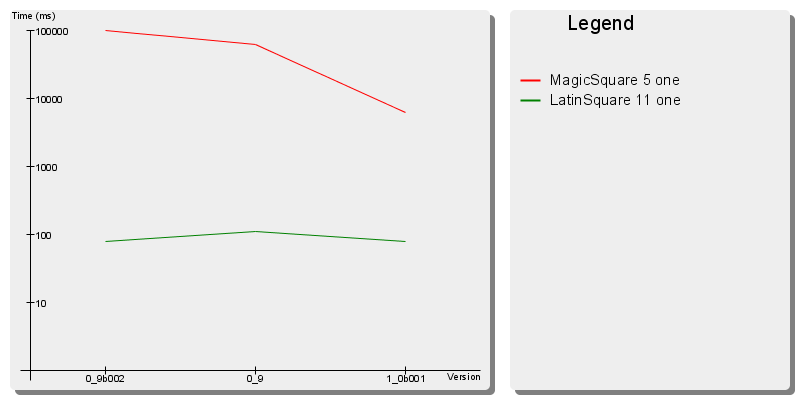
Magic Square
The problem is modeled with N * N integer variables of domain 1 .. N * N corresponding to each cell of the square, and linear combinations are posted for each line, each column and the two diagonals (the magic number is given a priori).
Golomb Rules
N variable for all distances (all pairs of mark) are used. Differences between all distances are stated with a BoundAllDiff constraint. Moreover, a global redondant constraint is added. The variable selection is done in the order of distances (from 0 to 1,2,3, then from 1 to 2,3,4, etc ...) : the first non instantiated distance is choosen.
Latin Square
The problem is modeled with N * N integer variables of domain 1 .. N corresponding to each cell of the square, and uses simple inequalities between variables of the same line and column.
Last Version Performance (in ms)
| Problems | MAC | CBJ | MACDBT | DR |
|---|---|---|---|---|
| MagicSquare 4 all | 45641 | 241781 | N/A | N/A |
| MagicSquare 5 one | 688 | 1656 | 16578 | 6281 |
| NQueens 12 all | 11532 | 52235 | 427922 | N/A |
| NQueens 13 all | 59688 | 298015 | N/A | N/A |
| NQueens 14 all | 352704 | N/A | N/A | N/A |
| GolombProblem 11 one | 101078 | N/A | N/A | N/A |
| GolombProblem 12 one | 970484 | N/A | N/A | N/A |
| LatinSquare 11 one | N/A | 47 | 78 | 78 |